What Change Will Be Caused By The Addition Of A Small Amount Of Hcl To A Hf/naf Buffer?

Chapter 14. Acrid-Base of operations Equilibria

xiv.6 Buffers

Learning Objectives

By the end of this section, you volition be able to:

• Describe the composition and function of acid–base of operations buffers
• Calculate the pH of a buffer before and after the addition of added acrid or base

A mixture of a weak acid and its cohabit base of operations (or a mixture of a weak base and its conjugate acid) is called a buffer solution, or a buffer. Buffer solutions resist a alter in pH when small amounts of a strong acrid or a potent base are added (Effigy 1). A solution of acetic acrid and sodium acetate (CH₃COOH + CH₃COONa) is an example of a buffer that consists of a weak acid and its salt. An example of a buffer that consists of a weak base and its salt is a solution of ammonia and ammonium chloride (NH₃(aq) + NH₄Cl(aq)).

Figure 1. (a) The buffered solution on the left and the unbuffered solution on the right have the same pH (pH 8); they are bones, showing the yellow color of the indicator methyl orange at this pH. (b) Later on the addition of 1 mL of a 0.01-K HCl solution, the buffered solution has non detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in colour of the methyl orange, which turns cerise at a pH of nearly 4. (credit: modification of work past Mark Ott)

How Buffers Piece of work

A mixture of acerb acrid and sodium acetate is acidic because the K _a of acetic acid is greater than the Yard _b of its cohabit base acetate. It is a buffer because it contains both the weak acid and its table salt. Hence, it acts to keep the hydronium ion concentration (and the pH) near constant by the addition of either a small-scale amount of a strong acid or a stiff base. If nosotros add a base of operations such every bit sodium hydroxide, the hydroxide ions react with the few hydronium ions nowadays. Then more of the acerb acid reacts with water, restoring the hydronium ion concentration well-nigh to its original value:

[latex]\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(50)\;{\longrightarrow}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)[/latex]

The pH changes very little. If we add an acid such equally hydrochloric acid, most of the hydronium ions from the muriatic acid combine with acetate ions, forming acetic acid molecules:

[latex]\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)\;{\longrightarrow}\;\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(l)[/latex]

Thus, there is very little increase in the concentration of the hydronium ion, and the pH remains practically unchanged (Effigy two).

Figure ii. This diagram shows the buffer action of these reactions.

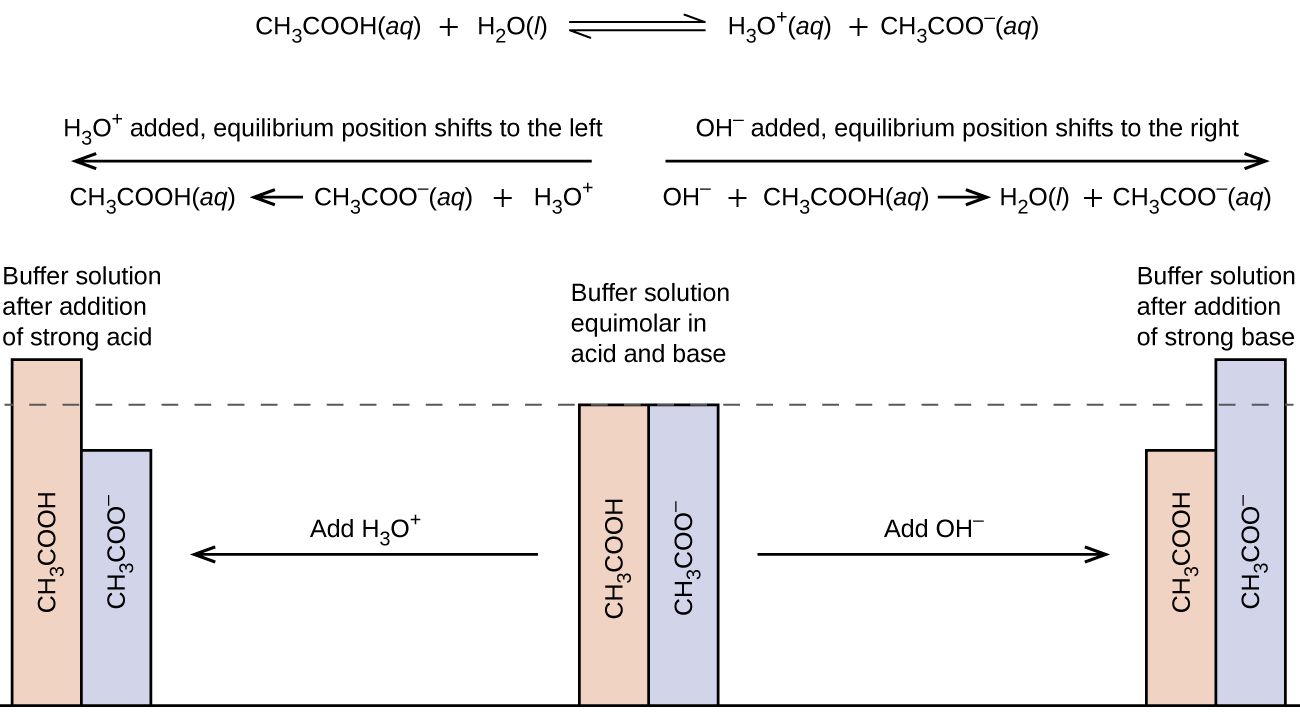
A mixture of ammonia and ammonium chloride is basic because the K _b for ammonia is greater than the Yard _a for the ammonium ion. Information technology is a buffer because information technology too contains the salt of the weak base. If we add together a base (hydroxide ions), ammonium ions in the buffer react with the hydroxide ions to form ammonia and water and reduce the hydroxide ion concentration almost to its original value:

[latex]\text{NH}_4^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq)\;{\longrightarrow}\;\text{NH}_3(aq)\;+\;\text{H}_2\text{O}(l)[/latex]

If nosotros add an acrid (hydronium ions), ammonia molecules in the buffer mixture react with the hydronium ions to course ammonium ions and reduce the hydronium ion concentration almost to its original value:

[latex]\text{H}_3\text{O}^{+}(aq)\;+\;\text{NH}_3(aq)\;{\longrightarrow}\;\text{NH}_4^{\;\;+}(aq)\;+\;\text{H}_2\text{O}(l)[/latex]

The three parts of the following instance illustrate the change in pH that accompanies the addition of base to a buffered solution of a weak acid and to an unbuffered solution of a strong acid.

Instance ane

pH Changes in Buffered and Unbuffered Solutions
Acetate buffers are used in biochemical studies of enzymes and other chemic components of cells to prevent pH changes that might alter the biochemical activity of these compounds.

(a) Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acrid and 0.10 M sodium acetate.

Solution
To determine the pH of the buffer solution we use a typical equilibrium calculation (as illustrated in earlier Examples):

1. Determine the direction of alter. The equilibrium in a mixture of H_threeO⁺, [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex], and CH₃CO₂H is:

   [latex]\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)[/latex]

   The equilibrium constant for CH_iiiCO_iiH is not given, so we look it up in Appendix H: 1000 _a = 1.eight × x^−v. With [CH₃CO₂H] = [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] = 0.10 One thousand and [H₃O⁺] = ~0 G, the reaction shifts to the right to course H₃O⁺.

2. Determine ten and equilibrium concentrations. A table of changes and concentrations follows:
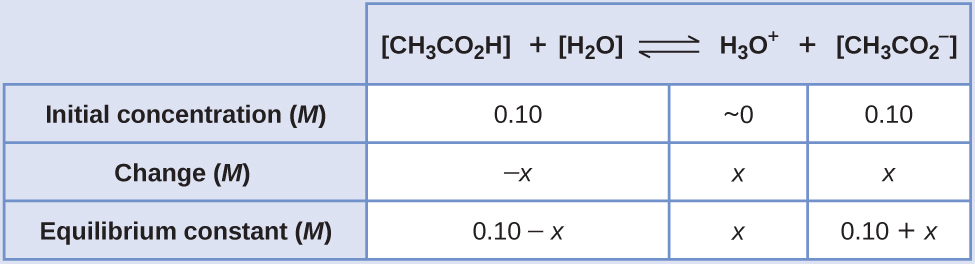
3. Solve for x and the equilibrium concentrations. We find:

   [latex]10 = i.eight\;\times\;10^{-5}\;K[/latex]

   and

   [latex][\text{H}_3\text{O}^{+}] = 0\;+\;10 = ane.8\;\times\;10^{-5}\;M[/latex]

   Thus:

   [latex]\text{pH} = -\text{log}[\text{H}_3\text{O}^{+}] = -\text{log}(i.viii\;\times\;10^{-5})[/latex]

   [latex]= 4.74[/latex]

4. Check the work. If nosotros calculate all calculated equilibrium concentrations, nosotros find that the equilibrium value of the reaction coefficient, Q = K _a.

(b) Calculate the pH subsequently 1.0 mL of 0.10 G NaOH is added to 100 mL of this buffer, giving a solution with a volume of 101 mL.

First, we calculate the concentrations of an intermediate mixture resulting from the complete reaction between the acrid in the buffer and the added base. So we determine the concentrations of the mixture at the new equilibrium:

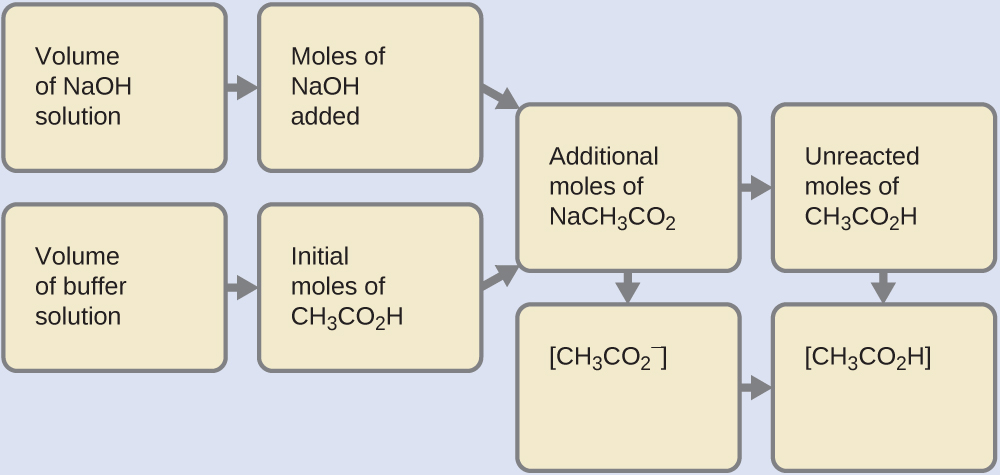
1. Decide the moles of NaOH. One milliliter (0.0010 L) of 0.10 Chiliad NaOH contains:

   [latex]0.0010\;\dominion[0.75ex]{0.7em}{0.1ex}\hspace{-0.7em}\text{L}\;\times\;(\frac{0.10\;\text{mol\;NaOH}}{1\;\rule[0.375ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L}}) = one.0\;\times\;10^{-4}\;\text{mol\;NaOH}[/latex]

2. Determine the moles of CH₂CO₂H. Earlier reaction, 0.100 L of the buffer solution contains:

   [latex]0.100\;\dominion[0.75ex]{0.7em}{0.1ex}\hspace{-0.7em}\text{L}\;\times\;(\frac{0.100\;\text{mol\;CH}_3\text{CO}_2\text{H}}{i\;\rule[0.375ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L}}) = 1.00\;\times\;10^{-2}\;\text{mol\;CH}_3\text{CO}_2\text{H}[/latex]

3. Solve for the amount of NaCH₃CO₂ produced. The 1.0 × 10⁻⁴ mol of NaOH neutralizes 1.0 × x⁻⁴ mol of CH_threeCO₂H, leaving:

   [latex](one.0\;\times\;10^{-2})\;-\;(0.01\;\times\;ten^{-2}) = 0.99\;\times\;ten^{-ii}\;\text{mol\;CH}_3\text{CO}_2\text{H}[/latex]

   and producing i.0 × 10^−four mol of NaCH₃CO₂. This makes a total of:

   [latex](1.0\;\times\;10^{-2})\;+\;(0.01\;\times\;10^{-2}) = 1.01\;\times\;10^{-2}\;\text{mol\;NaCH}_3\text{CO}_2[/latex]

4. Find the molarity of the products. After reaction, CH_iiiCO₂H and NaCH₃CO₂ are contained in 101 mL of the intermediate solution, and so:

   [latex][\text{CH}_3\text{CO}_2\text{H}] = \frac{9.9\;\times\;10^{-3}\;\text{mol}}{0.101\;\text{L}} = 0.098\;M[/latex]

   [latex][\text{NaCH}_3\text{CO}_2] = \frac{1.01\;\times\;10^{-2}\;\text{mol}}{0.101\;\text{L}} = 0.100\;Chiliad[/latex]

   Now we calculate the pH after the intermediate solution, which is 0.098 G in CH₃CO_iiH and 0.100 M in NaCH₃CO₂, comes to equilibrium. The calculation is very similar to that in part (a) of this example:

   

   This series of calculations gives a pH = 4.75. Thus the improver of the base barely changes the pH of the solution (Figure 1).

(c) For comparison, summate the pH after 1.0 mL of 0.10 Yard NaOH is added to 100 mL of a solution of an unbuffered solution with a pH of 4.74 (a 1.eight × 10⁻⁵–M solution of HCl). The book of the final solution is 101 mL.

Solution
This 1.8 × 10⁻⁵–M solution of HCl has the same hydronium ion concentration as the 0.x-Thou solution of acetic acid-sodium acetate buffer described in part (a) of this case. The solution contains:

[latex]0.100\;\text{L}\;\times\;(\frac{ane.8\;\times\;ten^{-five}\;\text{mol\;HCl}}{ane\;\text{L}}) = 1.8\;\times\;10^{-6}\;\text{mol\;HCl}[/latex]

As shown in part (b), 1 mL of 0.10 M NaOH contains 1.0 × 10^−iv mol of NaOH. When the NaOH and HCl solutions are mixed, the HCl is the limiting reagent in the reaction. All of the HCl reacts, and the corporeality of NaOH that remains is:

[latex](1.0\;\times\;10^{-4})\;-\;(ane.8\;\times\;ten^{-six}) = 9.viii\;\times\;10^{-5}\;Yard[/latex]

The concentration of NaOH is:

[latex]\frac{nine.8\;\times\;ten^{-5}\;M\;\text{NaOH}}{0.101\;\text{L}} = 9.seven\;\times\;10^{-4}\;M[/latex]

The pOH of this solution is:

[latex]\text{pOH} = -\text{log}[\text{OH}^{-}] = -\text{log}(9.7\;\times\;10^{-4}) = iii.01[/latex]

The pH is:

[latex]\text{pH} = fourteen.00\;-\;\text{pOH} = ten.99[/latex]

The pH changes from iv.74 to 10.99 in this unbuffered solution. This compares to the change of four.74 to iv.75 that occurred when the same amount of NaOH was added to the buffered solution described in role (b).

Bank check Your Learning
Prove that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a 1.viii × x^−v M HCl solution from 4.74 to three.00.

Answer:

Initial pH of 1.8 × 10⁻⁵ M HCl; pH = −log[H_iiiO⁺] = −log[1.8 × 10⁻⁵] = 4.74

Moles of H₃O⁺ in 100 mL 1.viii × 10⁻⁵ Thousand HCl; 1.viii × x⁻⁵ moles/Fifty × 0.100 L = 1.8 × 10⁻⁶

Moles of H_threeO⁺ added past addition of 1.0 mL of 0.x M HCl: 0.x moles/L × 0.0010 L = 1.0 × x⁻⁴ moles; terminal pH after addition of 1.0 mL of 0.10 M HCl:

[latex]\text{pH} = -\text{log}[\text{H}_3\text{O}^{+}] = -\text{log}(\frac{\text{total\;moles\;H}_3\text{O}^{+}}{\text{full\;volume}}) = -\text{log}(\frac{1.0\;\times\;10^{-4}\;\text{mol}\;+\;one.viii\;\times\;ten^{-6}\;\text{mol}}{101\;\text{mL}(\frac{1\;\text{L}}{grand\;\text{mL}})}) = iii.00[/latex]

If we add an acid or a base to a buffer that is a mixture of a weak base and its table salt, the calculations of the changes in pH are analogous to those for a buffer mixture of a weak acrid and its salt.

Buffer Capacity

Buffer solutions do not have an unlimited chapters to keep the pH relatively abiding (Figure iii). If nosotros add and so much base to a buffer that the weak acrid is wearied, no more buffering action toward the base is possible. On the other hand, if we add an excess of acid, the weak base would be exhausted, and no more than buffering action toward whatever additional acrid would be possible. In fact, we exercise not even demand to exhaust all of the acid or base in a buffer to overwhelm it; its buffering action will diminish rapidly as a given component nears depletion.

Figure iii. The indicator colour (methyl orangish) shows that a small amount of acid added to a buffered solution of pH 8 (beaker on the left) has little affect on the buffered system (center chalice). However, a large corporeality of acid exhausts the buffering capacity of the solution and the pH changes dramatically (chalice on the right). (credit: modification of work by Mark Ott)

The buffer chapters is the amount of acid or base that tin can be added to a given volume of a buffer solution earlier the pH changes significantly, usually by one unit. Buffer capacity depends on the amounts of the weak acrid and its conjugate base of operations that are in a buffer mixture. For example, 1 50 of a solution that is ane.0 M in acetic acid and one.0 M in sodium acetate has a greater buffer capacity than 1 L of a solution that is 0.10 M in acetic acid and 0.ten M in sodium acetate even though both solutions accept the same pH. The get-go solution has more buffer capacity because it contains more than acerb acid and acetate ion.

Selection of Suitable Buffer Mixtures

In that location are two useful rules of thumb for selecting buffer mixtures:

1. A skillful buffer mixture should take about equal concentrations of both of its components. A buffer solution has by and large lost its usefulness when 1 component of the buffer pair is less than about 10% of the other. Effigy 4 shows an acerb acid-acetate ion buffer as base is added. The initial pH is 4.74. A change of 1 pH unit occurs when the acetic acid concentration is reduced to 11% of the acetate ion concentration.
   

   

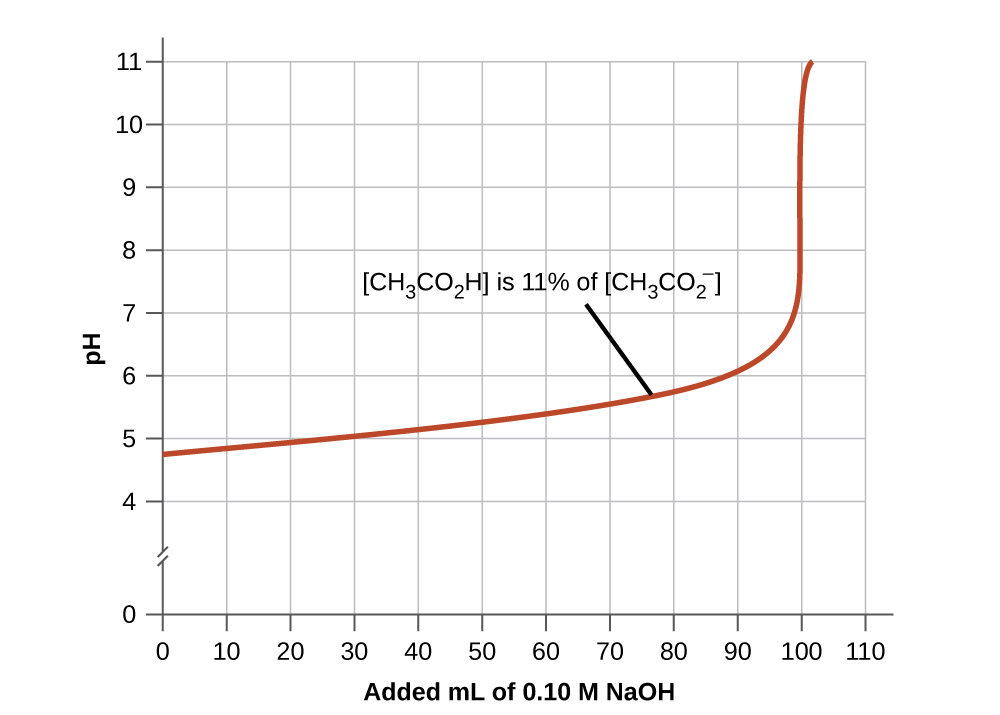
   Figure 4. The graph, an illustration of buffering action, shows alter of pH every bit an increasing amount of a 0.x-M NaOH solution is added to 100 mL of a buffer solution in which, initially, [CH₃CO_twoH] = 0.10 Chiliad and [CH₃CO₂ ⁻] = 0.x1000.

2. Weak acids and their salts are ameliorate every bit buffers for pHs less than seven; weak bases and their salts are better as buffers for pHs greater than 7.

Claret is an of import example of a buffered solution, with the principal acid and ion responsible for the buffering activeness existence carbonic acid, H₂CO₃, and the bicarbonate ion, [latex]\text{HCO}_3^{\;\;-}[/latex]. When an excess of hydrogen ion enters the blood stream, it is removed primarily by the reaction:

[latex]\text{H}_3\text{O}^{+}(aq)\;+\;\text{HCO}_3^{\;\;-}(aq)\;{\longrightarrow}\;\text{H}_2\text{CO}_3(aq)\;+\;\text{H}_2\text{O}(l)[/latex]

When an backlog of the hydroxide ion is present, information technology is removed by the reaction:

[latex]\text{OH}^{-}(aq)\;+\;\text{H}_2\text{CO}_3(aq)\;{\longrightarrow}\;\text{HCO}_3^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(l)[/latex]

The pH of man blood thus remains very near seven.35, that is, slightly bones. Variations are ordinarily less than 0.1 of a pH unit. A change of 0.4 of a pH unit is likely to be fatal.

The Henderson-Hasselbalch Equation

The ionization-constant expression for a solution of a weak acid can exist written as:

[latex]K_{\text{a}} = \frac{[\text{H}_3\text{O}^{+}][\text{A}^{-}]}{[\text{HA}]}[/latex]

Rearranging to solve for [H₃O⁺], we get:

[latex][\text{H}_3\text{O}^{+}] = K_{\text{a}}\;\times\;\frac{[\text{HA}]}{[\text{A}^{-}]}[/latex]

Taking the negative logarithm of both sides of this equation, we arrive at:

[latex]-\text{log}[\text{H}_3\text{O}^{+}] = -\text{log}\;K_{\text{a}}\;-\;\text{log}\frac{[\text{HA}]}{[\text{A}^{-}]}[/latex],

which tin be written every bit

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\frac{[\text{A}^{-}]}{[\text{HA}]}[/latex]

where pK _a is the negative of the common logarithm of the ionization abiding of the weak acid (pK _a = −log K _a). This equation relates the pH, the ionization abiding of a weak acid, and the concentrations of the weak acid and its salt in a buffered solution. Scientists frequently use this expression, called the Henderson-Hasselbalch equation, to calculate the pH of buffer solutions. It is important to note that the "10 is small" assumption must be valid to use this equation.

Lawrence Joseph Henderson and Karl Albert Hasselbalch

Lawrence Joseph Henderson (1878–1942) was an American physician, biochemist and physiologist, to name only a few of his many pursuits. He obtained a medical degree from Harvard and then spent 2 years studying in Strasbourg, then a function of Frg, before returning to accept a lecturer position at Harvard. He somewhen became a professor at Harvard and worked there his entire life. He discovered that the acid-base balance in human blood is regulated by a buffer system formed past the dissolved carbon dioxide in blood. He wrote an equation in 1908 to depict the carbonic acid-carbonate buffer arrangement in blood. Henderson was broadly knowledgeable; in add-on to his of import research on the physiology of blood, he also wrote on the adaptations of organisms and their fit with their environments, on sociology and on university teaching. He also founded the Fatigue Laboratory, at the Harvard Business School, which examined homo physiology with specific focus on work in industry, exercise, and nutrition.

In 1916, Karl Albert Hasselbalch (1874–1962), a Danish physician and chemist, shared authorship in a paper with Christian Bohr in 1904 that described the Bohr upshot, which showed that the power of hemoglobin in the blood to demark with oxygen was inversely related to the acidity of the blood and the concentration of carbon dioxide. The pH calibration was introduced in 1909 by some other Dane, Sørensen, and in 1912, Hasselbalch published measurements of the pH of claret. In 1916, Hasselbalch expressed Henderson's equation in logarithmic terms, consequent with the logarithmic calibration of pH, and thus the Henderson-Hasselbalch equation was built-in.

Medicine: The Buffer System in Blood

The normal pH of human claret is about vii.4. The carbonate buffer organisation in the blood uses the post-obit equilibrium reaction:

[latex]\text{CO}_2(chiliad)\;+\;2\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{CO}_3(aq)\;{\rightleftharpoons}\;\text{HCO}_3^{\;\;-}(aq)\;+\;\text{H}_3\text{O}^{+}(aq)[/latex]

The concentration of carbonic acid, H₂CO₃ is approximately 0.0012 M, and the concentration of the hydrogen carbonate ion, [latex]\text{HCO}_3^{\;\;-}[/latex], is around 0.024 M. Using the Henderson-Hasselbalch equation and the pK _a of carbonic acid at trunk temperature, we tin calculate the pH of blood:

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\frac{[\text{base}]}{[\text{acid}]} = six.4\;+\;\text{log}\frac{0.024}{0.0012} = 7.7[/latex]

The fact that the H₂CO₃ concentration is significantly lower than that of the [latex]\text{HCO}_3^{\;\;-}[/latex] ion may seem unusual, but this imbalance is due to the fact that nigh of the past-products of our metabolism that enter our bloodstream are acidic. Therefore, there must be a larger proportion of base of operations than acid, and so that the capacity of the buffer will not be exceeded.

Lactic acid is produced in our muscles when we practice. As the lactic acid enters the bloodstream, information technology is neutralized by the [latex]\text{HCO}_3^{\;\;-}[/latex] ion, producing H₂CO₃. An enzyme and so accelerates the breakdown of the backlog carbonic acid to carbon dioxide and h2o, which can be eliminated by breathing. In fact, in addition to the regulating effects of the carbonate buffering organization on the pH of blood, the torso uses breathing to regulate blood pH. If the pH of the blood decreases as well far, an increment in breathing removes CO₂ from the blood through the lungs driving the equilibrium reaction such that [H₃O⁺] is lowered. If the blood is as well alkaline, a lower breath charge per unit increases CO₂ concentration in the blood, driving the equilibrium reaction the other fashion, increasing [H⁺] and restoring an appropriate pH.

View data on the buffer system encountered in natural waters.

Key Concepts and Summary

A solution containing a mixture of an acid and its conjugate base, or of a base and its conjugate acid, is called a buffer solution. Unlike in the case of an acid, base, or salt solution, the hydronium ion concentration of a buffer solution does non alter greatly when a small amount of acid or base is added to the buffer solution. The base (or acid) in the buffer reacts with the added acid (or base).

Primal Equations

• pK _a = −log K _a
• p1000 _b = −log Thou _b
• [latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\frac{[\text{A}^{-}]}{[\text{HA}]}[/latex]

Chemistry Terminate of Chapter Exercises

1. Explain why a buffer can be prepared from a mixture of NH₄Cl and NaOH but not from NH₃ and NaOH.
2. Explain why the pH does not change significantly when a small corporeality of an acrid or a base is added to a solution that contains equal amounts of the acid H₃PO₄ and a table salt of its conjugate base NaH_twoPO₄.
3. Explicate why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the base of operations NH_iii and a common salt of its conjugate acid NH₄Cl.
4. What is [H₃O⁺] in a solution of 0.25 Chiliad CH₃CO₂H and 0.030 M NaCH₃CO_ii?
   [latex]\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(50)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)\;\;\;\;\;\;\;K_{\text{a}} = 1.8\;\times\;10^{-5}[/latex]
5. What is [H₃O⁺] in a solution of 0.075 M HNO_ii and 0.030 Grand NaNO₂?
   [latex]\text{HNO}_2(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{NO}_2^{\;\;-}(aq)\;\;\;\;\;\;\;K_{\text{a}} = iv.5\;\times\;10^{-5}[/latex]
6. What is [OH⁻] in a solution of 0.125 M CH₃NH_ii and 0.130 M CH₃NH₃Cl?
   [latex]\text{CH}_3\text{NH}_2(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{CH}_3\text{NH}_3^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{b}} = four.four\;\times\;x^{-4}[/latex]
7. What is [OH⁻] in a solution of i.25 M NH₃ and 0.78 Thousand NH_ivNO₃?
   [latex]\text{NH}_3(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{NH}_4^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq)\;\;\;\;\;\;\;K_{\text{b}} = 1.8\;\times\;x^{-5}[/latex]
8. What concentration of NH₄NO₃ is required to brand [OH⁻] = one.0 × 10⁻⁵ in a 0.200-K solution of NH₃?
9. What concentration of NaF is required to make [H_threeO⁺] = 2.3 × ten^−iv in a 0.300-M solution of HF?
10. What is the effect on the concentration of acetic acid, hydronium ion, and acetate ion when the following are added to an acidic buffer solution of equal concentrations of acetic acid and sodium acetate:

    (a) HCl

    (b) KCH_threeCO₂

    (c) NaCl

    (d) KOH

    (due east) CH₃CO_twoH

11. What is the outcome on the concentration of ammonia, hydroxide ion, and ammonium ion when the following are added to a basic buffer solution of equal concentrations of ammonia and ammonium nitrate:

    (a) KI

    (b) NH₃

    (c) How-do-you-do

    (d) NaOH

    (e) NH₄Cl

12. What will exist the pH of a buffer solution prepared from 0.20 mol NH₃, 0.twoscore mol NH_fourNO₃, and just enough h2o to give 1.00 L of solution?
13. Calculate the pH of a buffer solution prepared from 0.155 mol of phosphoric acrid, 0.250 mole of KH₂PO₄, and enough water to make 0.500 L of solution.
14. How much solid NaCH₃CO₂•3H₂O must exist added to 0.300 Fifty of a 0.l-Yard acetic acid solution to requite a buffer with a pH of 5.00? (Hint: Presume a negligible alter in volume as the solid is added.)
15. What mass of NH₄Cl must be added to 0.750 Fifty of a 0.100-M solution of NH₃ to requite a buffer solution with a pH of nine.26? (Hint: Assume a negligible change in volume as the solid is added.)
16. A buffer solution is prepared from equal volumes of 0.200 M acetic acrid and 0.600 M sodium acetate. Utilise 1.80 × ten⁻⁵ equally G _a for acerb acid.

    (a) What is the pH of the solution?

    (b) Is the solution acidic or basic?

    (c) What is the pH of a solution that results when 3.00 mL of 0.034 Yard HCl is added to 0.200 L of the original buffer?

17. A 5.36–k sample of NH_fourCl was added to 25.0 mL of 1.00 M NaOH and the resulting solution

    diluted to 0.100 L.

    (a) What is the pH of this buffer solution?

    (b) Is the solution acidic or basic?

    (c) What is the pH of a solution that results when iii.00 mL of 0.034 M HCl is added to the solution?

18. Which acid in Tabular array 2 in Chapter fourteen.3 Relative Strengths of Acids and Bases is almost appropriate for preparation of a buffer solution with a pH of 3.i? Explain your choice.
19. Which acid in Table ii in Chapter fourteen.three Relative Strengths of Acids and Bases is well-nigh appropriate for preparation of a buffer solution with a pH of 3.7? Explain your choice.
20. Which base of operations in Table 3 in Chapter 14.3 Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of ten.65? Explain your choice.
21. Which base in Tabular array 3 in Affiliate 14.3 Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of 9.20? Explain your option.
22. What is the pH of 1.000 Fifty of a solution of 100.0 g of glutamic acid (C₅H₉NO_iv, a diprotic acid; Chiliad ₁ = 8.5 × x⁻⁵, G _two = 3.39 × 10⁻¹⁰) to which has been added 20.0 thousand of NaOH during the grooming of monosodium glutamate, the flavoring agent? What is the pH when exactly 1 mol of NaOH per mole of acrid has been added?

Glossary

buffer chapters

amount of an acid or base that can be added to a volume of a buffer solution before its pH changes significantly (commonly by one pH unit)

buffer

mixture of a weak acrid or a weak base and the salt of its conjugate; the pH of a buffer resists change when modest amounts of acid or base are added

Henderson-Hasselbalch equation

equation used to calculate the pH of buffer solutions

Solutions

Answers to Chemical science End of Affiliate Exercises

2. Excess H₃O⁺ is removed primarily by the reaction:

[latex]\text{H}_3\text{O}^{+}(aq)\;+\;\text{H}_2\text{PO}_4^{\;\;-}(aq)\;{\longrightarrow}\;\text{H}_3\text{PO}_4(aq)\;+\;\text{H}_2\text{O}(50)[/latex]

Excess base is removed by the reaction:

[latex]\text{OH}^{-}(aq)\;+\;\text{H}_3\text{PO}_4(aq)\;{\longrightarrow}\;\text{H}_2\text{PO}_4^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(50)[/latex]

four. [H₃O⁺] = 1.five × 10⁻⁴ M

6. [OH⁻] = 4.2 × 10⁻⁴ M

8. [NH_fourNO₃] = 0.36 M

x. (a) The added HCl will increment the concentration of H₃O⁺ slightly, which will react with [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex] and produce CH₃CO_iiH in the process. Thus, [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] decreases and [CH₃CO₂H] increases.

(b) The added KCH₃CO₂ will increase the concentration of [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] which will react with H₃O⁺ and produce CH_threeCO_ii H in the process. Thus, [H₃O⁺] decreases slightly and [CH_threeCO_iiH] increases.

(c) The added NaCl will have no effect on the concentration of the ions.

(d) The added KOH will produce OH⁻ ions, which will react with the H₃O⁺, thus reducing [H₃O⁺]. Some additional CH_threeCO_iiH will dissociate, producing [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] ions in the process. Thus, [CH₃CO_twoH] decreases slightly and [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] increases.

(e) The added CH₃CO₂H will increment its concentration, causing more of it to dissociate and producing more [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] and H₃O⁺ in the procedure. Thus, [H_threeO⁺] increases slightly and [latex][\text{CH}_3\text{CO}_2^{\;\;-}][/latex] increases.

12. pH = 8.95

xiv. 37 m (0.27 mol)

sixteen. (a) pH = 5.222;

(b) The solution is acidic.

(c) pH = five.221

18. To ready the best buffer for a weak acid HA and its common salt, the ratio [latex]\frac{[\text{H}_3\text{O}^{+}]}{K_{\text{a}}}[/latex] should be every bit close to 1 as possible for constructive buffer activity. The [H₃O⁺] concentration in a buffer of pH iii.1 is [H₃O⁺] = 10^−three.1 = 7.94 × ten^−iv Thousand

We tin now solve for K _a of the all-time acid every bit follows:

[latex]\frac{[\text{H}_3\text{O}^{+}]}{K_{\text{a}}} = 1 \\[0.5em] K_{\text{a}} = \frac{[\text{H}_3\text{O}^{+}]}{i} = 7.94\;\times\;10^{-iv}[/latex]

In Table 2 in Chapter fourteen.3 Relative Strengths of Acids and Bases, the acid with the closest Grand _a to 7.94 × ten^−iv is HF, with a K _a of 7.2 × ten^−iv.

20. For buffers with pHs > 7, you should use a weak base and its salt. The most effective buffer volition have a ratio [latex]\frac{[\text{OH}^{-}]}{K_{\text{b}}}[/latex] that is equally shut to i every bit possible. The pOH of the buffer is fourteen.00 − 10.65 = three.35. Therefore, [OH⁻] is [OH⁻] = 10^−pOH = 10^−3.35 = iv.467 × 10⁻⁴ M.

We can now solve for Yard _b of the best base every bit follows:

[latex]\frac{[\text{OH}^{-}]}{K_{\text{b}}} = one[/latex]

M _b = [OH⁻] = iv.47 × x^−four

In Table 3 in Chapter 14.3 Relative Strengths of Acids and Bases, the base of operations with the closest Grand _b to 4.47 × x⁻⁴ is CH₃NH_ii, with a K _b = 4.4 × 10⁻⁴.

Source: https://opentextbc.ca/chemistry/chapter/14-6-buffers/

Posted by: coxhalight.blogspot.com

Share this post